Baru-baru ini keputusan yang sangat aneh telah membuat pusingan. Ia mengatakan bahawa apabila anda menambah semua nombor semula jadi
1 + 2 + 3 + 4 + ...
maka jawapan untuk jumlah ini adalah -1/12. Ide ini dipaparkan dalam video Numberphile (lihat di bawah ), yang mendakwa untuk membuktikan hasilnya dan juga mengatakan bahawa ia digunakan di seluruh tempat dalam fizik. Orang ramai mendapati idea itu begitu mengejutkan bahawa ia bahkan membuatnya menjadi New York Times . Jadi apa maksudnya?
Matematik
Pertama sekali, jumlah tidak terhingga semua nombor semulajadi tidak sama dengan -1/12.Anda boleh dengan mudah meyakinkan diri anda tentang ini dengan mengetik ke kalkulator anda jumlah separa
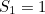
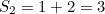
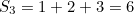
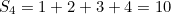

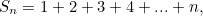
dan sebagainya. The 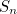 semakin besar dan lebih besar semakin besar
semakin besar dan lebih besar semakin besar 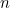 mendapat, iaitu nombor yang lebih semula jadi yang anda sertakan. Malah, anda boleh buat
mendapat, iaitu nombor yang lebih semula jadi yang anda sertakan. Malah, anda boleh buat 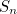 seberapa besar yang anda suka dengan memilih
seberapa besar yang anda suka dengan memilih 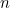 cukup besar. Sebagai contoh, untuk
cukup besar. Sebagai contoh, untuk 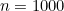 anda mendapatkan
anda mendapatkan
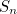 semakin besar dan lebih besar semakin besar
semakin besar dan lebih besar semakin besar 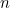 mendapat, iaitu nombor yang lebih semula jadi yang anda sertakan. Malah, anda boleh buat
mendapat, iaitu nombor yang lebih semula jadi yang anda sertakan. Malah, anda boleh buat 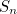 seberapa besar yang anda suka dengan memilih
seberapa besar yang anda suka dengan memilih 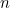 cukup besar. Sebagai contoh, untuk
cukup besar. Sebagai contoh, untuk 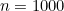 anda mendapatkan
anda mendapatkan![\ [S_ n = 500,500, \]](https://plus.maths.org/MI/df22fe35c1987e39a64d7f0ffa2d3e51/images/img-0010.png) |
dan untuk 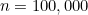 anda mendapatkan
anda mendapatkan
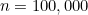 anda mendapatkan
anda mendapatkan![\ [S_ n = 5,000,050,000. \]](https://plus.maths.org/MI/df22fe35c1987e39a64d7f0ffa2d3e51/images/img-0012.png) |
Itulah sebabnya ahli matematik mengatakan bahawa jumlahnya
![\ [1 + 2 + 3 + 4 + ... \]](https://plus.maths.org/MI/b48eec2db5d26f324e8213f2b232e449/images/img-0001.png) |
menyimpang kepada infiniti. Atau, untuk meletakkannya lebih longgar, bahawa jumlahnya sama dengan infiniti.

Srinivasa Ramanujan
Jadi di manakah -1/12 datang? Hasil yang salah sebenarnya muncul dalam karya ahli matematik India terkenal Srinivasa Ramanujan pada tahun 1913 (lihat artikel ini untuk maklumat lanjut). Tetapi Ramanujan tahu apa yang dia lakukan dan mempunyai alasan untuk menulisnya. Dia telah bekerja pada apa yang dipanggil fungsi Euler zeta . Untuk memahami apa itu, pertama pertimbangkan jumlah yang tidak terhingga
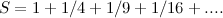
Anda mungkin mengiktiraf ini sebagai jumlah yang anda dapat apabila anda mengambil setiap nombor semula jadi, segi empat, dan kemudian mengambil balasan:
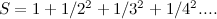
Sekarang jumlah ini tidak menyimpang. Jika anda mengambil urutan jumlah separa seperti yang kita lakukan di atas,
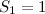
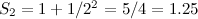
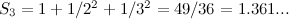

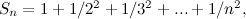
maka keputusan yang anda dapatkan dengan sewenang-wenangnya, tidak pernah melebihi, jumlahnya 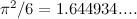 Ahli matematik mengatakan jumlah itu berkumpul
Ahli matematik mengatakan jumlah itu berkumpul 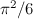 , atau lebih longgar, bahawa ia sama
, atau lebih longgar, bahawa ia sama 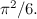
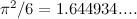 Ahli matematik mengatakan jumlah itu berkumpul
Ahli matematik mengatakan jumlah itu berkumpul 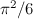 , atau lebih longgar, bahawa ia sama
, atau lebih longgar, bahawa ia sama 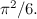
Sekarang apa yang berlaku apabila bukannya menaikkan nombor semula jadi dalam penyebut kepada kuasa 2, anda membangkitkannya kepada beberapa kuasa lain  ? Ternyata jumlah yang sepadan
? Ternyata jumlah yang sepadan
 ? Ternyata jumlah yang sepadan
? Ternyata jumlah yang sepadan![\ [S (x) = 1 + 1/2 ^ x + 1/3 ^ x + 1/4 ^ x ... \]](https://plus.maths.org/MI/3f5cf5a26d378c0d91a207c4a1255c7f/images/img-0012.png) |
menumpuk kepada nilai terhingga selagi kuasa  adalah nombor yang lebih besar daripada
adalah nombor yang lebih besar daripada 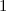 .Untuk setiap
.Untuk setiap 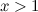 , ekspresi
, ekspresi 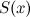 mempunyai nilai yang terhingga dan terhingga.
mempunyai nilai yang terhingga dan terhingga. 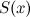 adalah apa yang dipanggil fungsi , dan ia dipanggil fungsi Euler zeta selepas ahli matematik abad ke-17 Leonhard Euler yang produktif.
adalah apa yang dipanggil fungsi , dan ia dipanggil fungsi Euler zeta selepas ahli matematik abad ke-17 Leonhard Euler yang produktif.
 adalah nombor yang lebih besar daripada
adalah nombor yang lebih besar daripada 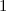 .Untuk setiap
.Untuk setiap 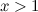 , ekspresi
, ekspresi 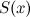 mempunyai nilai yang terhingga dan terhingga.
mempunyai nilai yang terhingga dan terhingga. 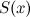 adalah apa yang dipanggil fungsi , dan ia dipanggil fungsi Euler zeta selepas ahli matematik abad ke-17 Leonhard Euler yang produktif.
adalah apa yang dipanggil fungsi , dan ia dipanggil fungsi Euler zeta selepas ahli matematik abad ke-17 Leonhard Euler yang produktif.
Setakat ini, sangat baik. Tetapi apa yang berlaku apabila anda memasukkan nilai  yang kurang daripada 1? Sebagai contoh, bagaimana jika anda memasuki
yang kurang daripada 1? Sebagai contoh, bagaimana jika anda memasuki 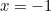 ? Mari lihat.
? Mari lihat.
 yang kurang daripada 1? Sebagai contoh, bagaimana jika anda memasuki
yang kurang daripada 1? Sebagai contoh, bagaimana jika anda memasuki 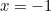 ? Mari lihat.
? Mari lihat.![\ [S (-1) = 1 + 1/2 ^ {- 1} +1/3 ^ {- 1} +1/4 ^ {- 1} ... \]](https://plus.maths.org/MI/2b5df501aae647079e305b7f698f8180/images/img-0003.png) |
![\ [= 1 + 2 + 3 + 4 + .... \]](https://plus.maths.org/MI/2b5df501aae647079e305b7f698f8180/images/img-0004.png) |
Jadi anda pulih jumlah asal kami, yang, seperti yang kita tahu, menyimpang. Begitu juga dengan nilai-nilai lain  kurang daripada atau sama dengan 1: jumlah diverges.
kurang daripada atau sama dengan 1: jumlah diverges.
 kurang daripada atau sama dengan 1: jumlah diverges.
kurang daripada atau sama dengan 1: jumlah diverges.Memperluaskan fungsi zeta Euler
Oleh kerana ia berfungsi fungsi Euler zeta S (x)ditakrifkan untuk bilangan sebenar x yang lebih besar daripada 1. Nombor sebenar adalah sebahagian daripada nombor keluarga yang lebih besar yang dikenali sebagai nombor kompleks .Dan sementara bilangan sebenar sesuai dengan semua titik di sepanjang garis panjang yang tidak terhingga, nombor kompleks sesuai dengan semua titik pada satah, yang mengandungi garis nombor sebenar. Pesawat itu dipanggil pesawat kompleks. Sama seperti anda boleh menentukan fungsi yang mengambil nombor sebenar sebagai input, anda boleh menentukan fungsi yang mengambil nombor kompleks sebagai input.
Satu perkara yang mengagumkan mengenai fungsi nombor kompleks ialah jika anda mengetahui fungsi yang cukup baik untuk beberapa set input, maka (sehingga beberapa butiran teknikal) anda dapat mengetahui nilai fungsi di mana-mana di pesawat kompleks.Kaedah memperluaskan definisi fungsi dikenali sebagai kesinambungan analitik . Fungsi Euler zeta ditakrifkan untuk nombor nyata yang lebih besar daripada 1. Oleh kerana bilangan sebenar juga nombor kompleks, kita dapat menganggapnya sebagai fungsi kompleks dan kemudian menerapkan penerusan analitik untuk mendapatkan fungsi baru, yang ditakrifkan di seluruh satah tetapi bersetuju dengan Euler fungsi zeta untuk nombor nyata lebih besar daripada 1. Itu fungsi Riemann zeta.
Tetapi ada juga perkara lain yang boleh anda lakukan.Menggunakan beberapa matematik bertenaga tinggi (dikenali sebagai analisis yang rumit , lihat kotak) ada cara memperluaskan definisi fungsi Euler zeta kepada nombor  kurang daripada atau sama dengan 1 dengan cara yang memberikan anda nilai terhingga. Dengan kata lain, terdapat cara untuk menentukan fungsi baru, memanggilnya
kurang daripada atau sama dengan 1 dengan cara yang memberikan anda nilai terhingga. Dengan kata lain, terdapat cara untuk menentukan fungsi baru, memanggilnya 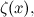 supaya untuk
supaya untuk 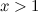
 kurang daripada atau sama dengan 1 dengan cara yang memberikan anda nilai terhingga. Dengan kata lain, terdapat cara untuk menentukan fungsi baru, memanggilnya
kurang daripada atau sama dengan 1 dengan cara yang memberikan anda nilai terhingga. Dengan kata lain, terdapat cara untuk menentukan fungsi baru, memanggilnya 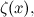 supaya untuk
supaya untuk 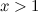
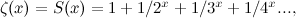
dan untuk 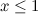 fungsinya
fungsinya 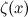 mempunyai nilai yang terhingga dan terhingga. Kaedah pelanjutan ini dinamakan kesinambungan analitik dan fungsi baru yang anda panggil dipanggil fungsi Riemann zeta , selepas matematikian ke-18 ahli matematik Bernhard Riemann. (Membuat fungsi baru ini memberi anda nilai-nilai terhingga
mempunyai nilai yang terhingga dan terhingga. Kaedah pelanjutan ini dinamakan kesinambungan analitik dan fungsi baru yang anda panggil dipanggil fungsi Riemann zeta , selepas matematikian ke-18 ahli matematik Bernhard Riemann. (Membuat fungsi baru ini memberi anda nilai-nilai terhingga 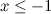 melibatkan cerdik mengecilkan jumlah yang berbeza, sehingga infiniti dari jumlah penyelewengan pertama yang menolak infiniti dari jumlah yang berbeda memberi Anda sesuatu yang terbatas.)
melibatkan cerdik mengecilkan jumlah yang berbeza, sehingga infiniti dari jumlah penyelewengan pertama yang menolak infiniti dari jumlah yang berbeda memberi Anda sesuatu yang terbatas.)
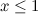 fungsinya
fungsinya 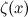 mempunyai nilai yang terhingga dan terhingga. Kaedah pelanjutan ini dinamakan kesinambungan analitik dan fungsi baru yang anda panggil dipanggil fungsi Riemann zeta , selepas matematikian ke-18 ahli matematik Bernhard Riemann. (Membuat fungsi baru ini memberi anda nilai-nilai terhingga
mempunyai nilai yang terhingga dan terhingga. Kaedah pelanjutan ini dinamakan kesinambungan analitik dan fungsi baru yang anda panggil dipanggil fungsi Riemann zeta , selepas matematikian ke-18 ahli matematik Bernhard Riemann. (Membuat fungsi baru ini memberi anda nilai-nilai terhingga 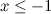 melibatkan cerdik mengecilkan jumlah yang berbeza, sehingga infiniti dari jumlah penyelewengan pertama yang menolak infiniti dari jumlah yang berbeda memberi Anda sesuatu yang terbatas.)
melibatkan cerdik mengecilkan jumlah yang berbeza, sehingga infiniti dari jumlah penyelewengan pertama yang menolak infiniti dari jumlah yang berbeda memberi Anda sesuatu yang terbatas.)
OKEY. Jadi sekarang kita mempunyai fungsi 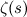 yang bersetuju dengan fungsi zeta Euler
yang bersetuju dengan fungsi zeta Euler 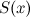 apabila anda memasukkan nilai
apabila anda memasukkan nilai 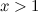 . Apabila anda memasukkan nilai
. Apabila anda memasukkan nilai 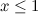 , fungsi zeta memberikan keluaran terhingga. Nilai apa yang anda dapati apabila anda memasangkannya
, fungsi zeta memberikan keluaran terhingga. Nilai apa yang anda dapati apabila anda memasangkannya 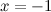 ke dalam fungsi zeta? Anda telah meneka:
ke dalam fungsi zeta? Anda telah meneka:
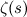 yang bersetuju dengan fungsi zeta Euler
yang bersetuju dengan fungsi zeta Euler 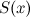 apabila anda memasukkan nilai
apabila anda memasukkan nilai 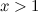 . Apabila anda memasukkan nilai
. Apabila anda memasukkan nilai 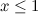 , fungsi zeta memberikan keluaran terhingga. Nilai apa yang anda dapati apabila anda memasangkannya
, fungsi zeta memberikan keluaran terhingga. Nilai apa yang anda dapati apabila anda memasangkannya 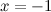 ke dalam fungsi zeta? Anda telah meneka:
ke dalam fungsi zeta? Anda telah meneka:![\ [\ zeta (-1) = - 1/12. \]](https://plus.maths.org/MI/07cd90a274a5617072ce0c507799e97d/images/img-0012.png) |
Sekiranya anda kini membuat kesilapan untuk mempercayai perkara itu 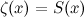 untuk
untuk 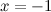 , maka anda mendapat ekspresi (salah)
, maka anda mendapat ekspresi (salah)
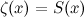 untuk
untuk 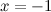 , maka anda mendapat ekspresi (salah)
, maka anda mendapat ekspresi (salah)![\ [S (-1) = 1 + 2 + 3 + 4 + ... = \ zeta (-1) = -1/12. \]](https://plus.maths.org/MI/07cd90a274a5617072ce0c507799e97d/images/img-0014.png) |
Inilah salah satu cara untuk memahami ungkapan misteri Ramanujan.
Silap mata
Jadi, bagaimanakah orang-orang dalam video Numberphile "membuktikan" bahawa nombor semula jadi semua menambah sehingga -1/12? Jawapan sebenar ialah mereka tidak. Menonton video itu seperti menyaksikan seorang ahli silap mata dan cuba melihat mereka menyelinap arnab ke dalam topi. Langkah salah satu "bukti" cuba memujuk anda sesuatu yang agak bodoh, iaitu jumlah yang tidak terhingga
![\ [1-1 + 1-1 + 1 -.... \]](https://plus.maths.org/MI/9259591c203fcddee6821b72d92159ca/images/img-0001.png) |
adalah sama dengan 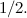
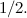
Video itu tidak tahan lama dan ini menyedarkannya. Tetapi mari kita lihat sedikit lebih dekat untuk melihat sama ada ia masuk akal sama sekali. Katakan bahawa jumlahnya 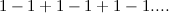 mempunyai nilai terhingga dan memanggilnya
mempunyai nilai terhingga dan memanggilnya 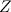 . Menambah
. Menambah 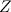 untuk dirinya sendiri anda mendapat jumlah yang tidak terhingga
untuk dirinya sendiri anda mendapat jumlah yang tidak terhingga
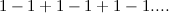 mempunyai nilai terhingga dan memanggilnya
mempunyai nilai terhingga dan memanggilnya 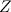 . Menambah
. Menambah 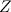 untuk dirinya sendiri anda mendapat jumlah yang tidak terhingga
untuk dirinya sendiri anda mendapat jumlah yang tidak terhingga![\ [Z + Z = 1-1 + 1-1 + 1 -.... + 1-1 + 1-1 + 1 -.... \]](https://plus.maths.org/MI/9259591c203fcddee6821b72d92159ca/images/img-0005.png) |
Tetapi ini hanya jumlah asal, menyiratkan
![\ [Z + Z = 2Z = Z. \]](https://plus.maths.org/MI/9259591c203fcddee6821b72d92159ca/images/img-0006.png) |
Sejak 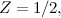 ia mengikutinya
ia mengikutinya 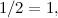 yang tidak masuk akal. Jadi pernyataan bahawa jumlah tak terhingga
yang tidak masuk akal. Jadi pernyataan bahawa jumlah tak terhingga 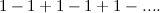 boleh diambil sama dengan 1/2 tidak betul. Sebenarnya, anda boleh memperoleh pelbagai hasil yang mengacaukan dengan jumlah wang yang tak terbatas yang menyimpang. Ia satu helah!
boleh diambil sama dengan 1/2 tidak betul. Sebenarnya, anda boleh memperoleh pelbagai hasil yang mengacaukan dengan jumlah wang yang tak terbatas yang menyimpang. Ia satu helah!
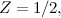 ia mengikutinya
ia mengikutinya 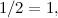 yang tidak masuk akal. Jadi pernyataan bahawa jumlah tak terhingga
yang tidak masuk akal. Jadi pernyataan bahawa jumlah tak terhingga 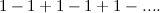 boleh diambil sama dengan 1/2 tidak betul. Sebenarnya, anda boleh memperoleh pelbagai hasil yang mengacaukan dengan jumlah wang yang tak terbatas yang menyimpang. Ia satu helah!
boleh diambil sama dengan 1/2 tidak betul. Sebenarnya, anda boleh memperoleh pelbagai hasil yang mengacaukan dengan jumlah wang yang tak terbatas yang menyimpang. Ia satu helah!Fizik
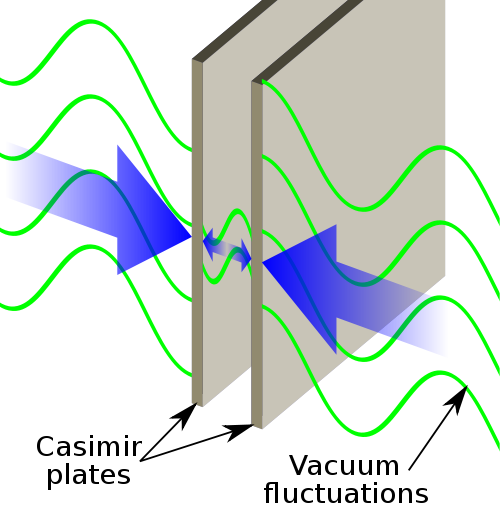
Tetapi bagaimanakah keputusan yang aneh dan yang salah ini menjadikannya buku teks fizik, seperti yang ditunjukkan dalam video? Di sinilah perkara benar-benar menarik. Katakan anda mengambil dua plat metalik dan susunnya dalam vakum supaya ia selari dengan satu sama lain.Menurut fizik klasik, tidak sepatutnya ada kekuatan bersih yang bertindak di antara kedua-dua plat itu.
Tetapi fizik klasik tidak menghitung dengan kesan pelik yang anda lihat apabila anda melihat dunia dengan skala yang sangat kecil. Untuk melakukan itu, anda memerlukan fizik kuantum, yang memberitahu kita banyak perkara yang sangat pelik. Salah satunya adalah bahawa vakum tidak kosong, tetapi bergetar dengan aktiviti. Apa yang dipanggil zarah-zarah mayamuncul dalam dan keluar dari masa ke masa. Aktiviti ini memberikan tenaga yang disebut titik sifar : tenagaterendah yang boleh dimiliki tidak pernah sifar (lihat di sini untuk lebih terperinci).
Apabila anda cuba mengira ketumpatan tenaga di antara kedua-dua plat menggunakan matematik fizik kuantum, anda akan memperoleh jumlah tak terhingga
![\ [1 + 8 + 27 + 64 + .... \]](https://plus.maths.org/MI/f95bbd3e72a4ff4bcfa9b87a485c0377/images/img-0001.png) |
Jumlah tak terhingga ini juga apa yang anda dapat apabila anda memasukkan nilai 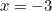 ke dalam fungsi Euler zeta:
ke dalam fungsi Euler zeta:
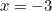 ke dalam fungsi Euler zeta:
ke dalam fungsi Euler zeta: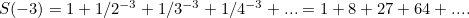
Itu malangnya, kerana jumlahnya menyimpang (ia lebih cepat daripada daripada 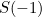 ), yang akan membayangkan ketumpatan tenaga tak terhingga. Ini jelas tidak masuk akal. Tetapi bagaimana jika anda cheekily menganggap bahawa jumlah tak terhingga sama dengan fungsi Riemann zeta, bukannya fungsi Euler zeta, yang dinilai pada
), yang akan membayangkan ketumpatan tenaga tak terhingga. Ini jelas tidak masuk akal. Tetapi bagaimana jika anda cheekily menganggap bahawa jumlah tak terhingga sama dengan fungsi Riemann zeta, bukannya fungsi Euler zeta, yang dinilai pada 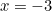 ? Nah, maka anda mendapat ketumpatan tenaga yang terhingga. Itu bermakna perlu ada daya yang menarik antara plat logam, yang juga nampaknya menggelikan, kerana fizik klasik mencadangkan tidak ada kekuatan.
? Nah, maka anda mendapat ketumpatan tenaga yang terhingga. Itu bermakna perlu ada daya yang menarik antara plat logam, yang juga nampaknya menggelikan, kerana fizik klasik mencadangkan tidak ada kekuatan.
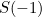 ), yang akan membayangkan ketumpatan tenaga tak terhingga. Ini jelas tidak masuk akal. Tetapi bagaimana jika anda cheekily menganggap bahawa jumlah tak terhingga sama dengan fungsi Riemann zeta, bukannya fungsi Euler zeta, yang dinilai pada
), yang akan membayangkan ketumpatan tenaga tak terhingga. Ini jelas tidak masuk akal. Tetapi bagaimana jika anda cheekily menganggap bahawa jumlah tak terhingga sama dengan fungsi Riemann zeta, bukannya fungsi Euler zeta, yang dinilai pada 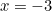 ? Nah, maka anda mendapat ketumpatan tenaga yang terhingga. Itu bermakna perlu ada daya yang menarik antara plat logam, yang juga nampaknya menggelikan, kerana fizik klasik mencadangkan tidak ada kekuatan.
? Nah, maka anda mendapat ketumpatan tenaga yang terhingga. Itu bermakna perlu ada daya yang menarik antara plat logam, yang juga nampaknya menggelikan, kerana fizik klasik mencadangkan tidak ada kekuatan.
Tetapi inilah kejutan. Apabila ahli fizik membuat eksperimen mereka mendapati bahawa daya itu wujud - dan ia sepadan dengan ketumpatan tenaga yang sama dengannya 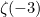 !
!
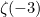 !
!
Hasil fizikal yang mengejutkan ini dikenali sebagai kesan Casimir , selepas fizik Belanda Hendrik Casimir.
Luangkan masa untuk mengambil ini. Fizik kuantum mengatakan ketumpatan tenaga perlu
![\ [S (-3) = 1 + 8 + 27 + 64 + .... \]](https://plus.maths.org/MI/a73c5a952304021cbae1e2d091f151fa/images/img-0001.png) |
Itulah karut, tetapi eksperimen menunjukkan bahawa jika anda (salah) menganggap jumlah ini sebagai fungsi zeta 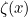 dinilai pada
dinilai pada 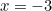 , anda mendapat jawapan yang betul. Jadi nampaknya sifat telah mengikuti idea yang kami jelaskan di atas. Ia memperluaskan fungsi Euler zeta untuk memasukkan nilai untuk
, anda mendapat jawapan yang betul. Jadi nampaknya sifat telah mengikuti idea yang kami jelaskan di atas. Ia memperluaskan fungsi Euler zeta untuk memasukkan nilai untuk  yang kurang dari 1, dengan bijak mengurangkan tak terbatas, dan sebagainya datang dengan nilai terhingga. Itu luar biasa!
yang kurang dari 1, dengan bijak mengurangkan tak terbatas, dan sebagainya datang dengan nilai terhingga. Itu luar biasa!
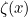 dinilai pada
dinilai pada 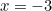 , anda mendapat jawapan yang betul. Jadi nampaknya sifat telah mengikuti idea yang kami jelaskan di atas. Ia memperluaskan fungsi Euler zeta untuk memasukkan nilai untuk
, anda mendapat jawapan yang betul. Jadi nampaknya sifat telah mengikuti idea yang kami jelaskan di atas. Ia memperluaskan fungsi Euler zeta untuk memasukkan nilai untuk  yang kurang dari 1, dengan bijak mengurangkan tak terbatas, dan sebagainya datang dengan nilai terhingga. Itu luar biasa!
yang kurang dari 1, dengan bijak mengurangkan tak terbatas, dan sebagainya datang dengan nilai terhingga. Itu luar biasa!
Sebab mengapa kita lihat 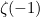 dan
dan 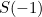 dalam video Numberphile dan buku teks fizik, bukannya
dalam video Numberphile dan buku teks fizik, bukannya  dan
dan 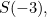 ialah apabila anda membayangkan kesan Casimir seperti yang berlaku dalam satu dimensi (sepanjang garis dan bukannya dalam 3D), kepadatan tenaga yang anda kira adalah
ialah apabila anda membayangkan kesan Casimir seperti yang berlaku dalam satu dimensi (sepanjang garis dan bukannya dalam 3D), kepadatan tenaga yang anda kira adalah 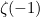 bukannya
bukannya  .
.
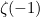 dan
dan 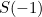 dalam video Numberphile dan buku teks fizik, bukannya
dalam video Numberphile dan buku teks fizik, bukannya  dan
dan 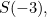 ialah apabila anda membayangkan kesan Casimir seperti yang berlaku dalam satu dimensi (sepanjang garis dan bukannya dalam 3D), kepadatan tenaga yang anda kira adalah
ialah apabila anda membayangkan kesan Casimir seperti yang berlaku dalam satu dimensi (sepanjang garis dan bukannya dalam 3D), kepadatan tenaga yang anda kira adalah 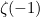 bukannya
bukannya  .
.
Jadi mengapa orang Numberphile mempublikasikan "hasil" pelik ini? Mereka pasti tahu mengenai kesinambungan analitik yang menjadikan fungsi itu jelas, tetapi itu sesuatu yang terlalu teknikal untuk video mereka. Mengetahui mereka mempunyai kaedah penerusan analitik, yang akan menjadikan keputusan akhir OK, tersembunyi di dalam poket belakang mereka, mereka meneruskan dengan tangan mereka. Dengan berbuat demikian mereka mendapat lebih daripada satu juta hits dan mempunyai dunia bercakap mengenai fungsi zeta dan matematik. Untuk ini mereka harus mengucapkan tahniah. Matematik fungsi zeta adalah hebat dan apa yang kita sebutkan di sini hanyalah permulaan senarai panjang sifat-sifat matematik yang luar biasa.Dalam membawa matematik dan fizik kepada orang ramai, kita sentiasa perlu membuat pilihan tentang apa yang kita tinggalkan dan apa yang kita jelaskan. Di mana untuk menarik garisan itu adalah sesuatu yang kita semua perlu meninggalkan hati nurani kita.