1 + 2 + 3 + 4 + ⋯

Empat empat jumlah pertama siri 1 + 2 + 3 + 4 + ⋯ . Parabola adalah asymptote terlicin mereka; y -interceptnya adalah -  1/12 . ^[1]

Siri tak terhingga yang seginya adalah nombor semulajadi1 + 2 + 3 + 4 + ⋯ adalah siri yang berbeza . Jumlah separa siri n adalah nombor segi tiga

$$ {\ displaystyle \ sum _ {k = 1} ^ {n} k = {\ frac {n (n + 1)} {2}},}

yang meningkat tanpa terikat sebagai n pergi ke tak terhingga . Kerana urutan jumlah separa gagal untuk menumpuk kepada had terhingga , siriini tidak mempunyai jumlah.

Walaupun siri ini seolah-olah pada pandangan pertama tidak mempunyai sebarang nilai yang bermakna, ia boleh dimanipulasi untuk menghasilkan beberapa hasil yang menarik secara matematik, yang sebahagiannya mempunyai aplikasi dalam bidang-bidang lain seperti analisis rumit  , Teori bidang kuantum , dan teori rentetan . Kaedah penjumlahan banyak digunakan dalam matematik untuk memberikan nilai berangka walaupun kepada siri yang berbeza. Khususnya, kaedah penamaan fungsi zeta dan penjumlahan Ramanujan memberikan siri nilai -  1/12 , yang dinyatakan oleh formula terkenal:

$$ {\ displaystyle 1 + 2 + 3 + 4 + \ cdots = - {\ frac {1} {12}},}

di mana sebelah kiri harus ditafsirkan sebagai nilai yang diperoleh dengan menggunakan salah satu kaedah penjumlahan yang disebutkan di atas dan bukan sebagai jumlah siri tak terhingga dalam makna biasa.

Dalam monografi pada teori moonshine , Terry Gannon menyebut persamaan ini "salah satu formula yang paling luar biasa dalam sains".

Jumlah separa [ sunting ]

Nombor enam segi tiga pertama

Artikel utama: Nombor segi tiga

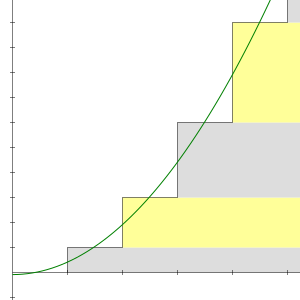
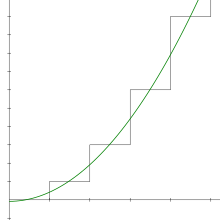
Jumlah separa siri 1 + 2 + 3 + 4 + 5 + 6 + ⋯ adalah 1, 3, 6, 10, 15 , dan sebagainya. Jumlah separa n diberikan dengan formula mudah:

$$ {\ displaystyle \ sum _ {k = 1} ^ {n} k = {\ frac {n (n + 1)} {2}}.}

Persamaan ini diketahui oleh Pythagoreans seawal abad keenam BCE. ^[4] Nombor bentuk ini dipanggil nombor segi tiga , kerana ia boleh diatur sebagai segitiga sama sisi.

Urutan tak terhingga nombor segi tiga berubah menjadi + ∞, jadi menurut definisi, siri tak terhingga 1 + 2 + 3 + 4 + ⋯ juga menyimpang ke + ∞. Divergensi adalah akibat yang sederhana dari bentuk siri: istilah tidak mendekati sifar, jadi siri ini menyimpang dari ujian istilah .

Summability [ sunting ]

Antara siri perpaduan klasik, 1 + 2 + 3 + 4 + ⋯ agak sukar untuk dimanipulasi menjadi nilai terhingga. Banyak kaedah penjumlahan digunakan untuk memberikan nilai berangka kepada siri yang berbeza, beberapa yang lebih berkuasa daripada yang lain. Sebagai contoh, penjumlahan Cesàro adalah satu kaedah yang terkenal yang merangkumi siri Grandi, siri yang agak berbeza 1 - 1 + 1 - 1 + ⋯ , hingga 1/2 . Penjumlahan Abel adalah satu kaedah yang lebih kuat yang tidak hanya merangkumkan siri Grandi kepada 1/2, tetapi juga merangkumi siri yang lebih rumit 1 - 2 + 3 - 4 + ⋯ hingga 1/4 .

Tidak seperti siri di atas, 1 + 2 + 3 + 4 + ⋯ tidak dapat disangkal Cesàro mahupun Abel boleh disimpulkan. Kaedah-kaedah ini bekerja pada siri yang berbeza-beza berayun, tetapi mereka tidak dapat menghasilkan jawapan yang terhingga untuk siri yang menyimpang kepada + ∞. ^[5] Sebilangan besar definisi yang lebih rendah daripada jumlah siri yang berbeza adalah stabil dan linier, dan sebarang kaedah yang stabil dan linier tidak boleh jumlah 1 + 2 + 3 + ⋯ ke nilai terhingga; lihat di bawah.Kaedah yang lebih maju diperlukan, seperti penamaan fungsi zeta atau penjumlahan Ramanujan . Ia juga mungkin untuk berhujah untuk nilai -  1/12 menggunakan beberapa heuristik kasar yang berkaitan dengan kaedah ini.

Heuristik [ sunting ]

Passage dari notebook pertama Ramanujan menggambarkan "tetap" siri ini

Srinivasa Ramanujan menyampaikan dua terbitan " 1 + 2 + 3 + 4 + ⋯ = -  1/12 "dalam bab 8 buku nota pertamanya. ^{[6] [7] [8]} Pencapaian yang lebih mudah, kurang ketat diperolehi dalam dua langkah, seperti berikut.

Wawasan utama pertama adalah bahawa siri nombor positif 1 + 2 + 3 + 4 + ⋯ hampir menyerupai silih ganti1 - 2 + 3 - 4 + ⋯ . Siri terakhir juga berbeza, tetapi lebih mudah untuk bekerja dengan; terdapat beberapa kaedah klasik yang memperuntukkan nilai, yang telah diterokai sejak abad ke-18. ^[9]

Untuk mengubah siri 1 + 2 + 3 + 4 + ⋯ ke 1 - 2 + 3 - 4 + ⋯ , satu dapat menolak 4 dari penggal kedua, 8 dari jangka keempat, 12 dari penggal keenam, dan sebagainya . Jumlah yang dikurangkan ialah 4 + 8 + 12 + 16 + ⋯ , iaitu 4 kali siri asal.Hubungan ini boleh dinyatakan menggunakan algebra. Walau apa pun "jumlah" siri ini, panggilnya c = 1 + 2 + 3 + 4 + ⋯.Kemudian kalikan persamaan ini dengan 4 dan tolak persamaan kedua dari yang pertama:

Wawasan utama kedua ialah siri silih ganti 1 - 2 + 3 - 4 + ⋯ ialah pengembangan siri kuasa formal fungsi 1/(1 + x ) ² tetapi dengan x ditakrifkan sebagai 1. Oleh itu, Ramanujan menulis:

$$ {\ displaystyle -3c = 1-2 + 3-4 + \ cdots = {\ frac {1} {(1 + 1) ^ {2}}} = {\ frac {1} {4}}}

Membahagikan kedua belah pihak dengan -3, satu mendapat c = -  1/12 .

Secara umumnya, adalah tidak betul untuk memanipulasi siri tak terhingga seolah-olah mereka adalah jumlah terhingga.Sebagai contoh, jika sifar dimasukkan ke dalam posisi sewenang-wenangnya dari siri yang berbeza, mungkin untuk mencapai keputusan yang tidak konsisten diri, apalagi konsisten dengan kaedah lain. Khususnya, langkah 4 c = 0 + 4 + 0 + 8 + ⋯ tidak dibenarkan oleh undang-undang identiti tambahan sahaja. Untuk contoh yang melampau, menambahkan sifar tunggal ke bahagian hadapan siri boleh menyebabkan keputusan yang tidak konsisten. ^[1]

Salah satu cara untuk memperbaiki keadaan ini, dan untuk menghalang tempat tempat sifar dapat dimasukkan, adalah untuk menjejaki setiap istilah dalam siri dengan melampirkan pergantungan pada beberapa fungsi. ^[10] Dalam siri 1 + 2 + 3 + 4 + ⋯ , setiap istilah n hanya nombor. Sekiranya istilah n dipromosikan ke fungsi n ^-s , di mana s adalah pembolehubah yang kompleks, maka seseorang dapat memastikan bahawa hanya istilah seperti yang ditambahkan. Siri yang dihasilkan mungkin dimanipulasi dengan cara yang lebih ketat, dan pembolehubah boleh ditetapkan kepada -1 kemudian. Pelaksanaan strategi ini disebut regulatariasi fungsi zeta .

Fungsi zeta regularization [ sunting ]

Plot ζ ( s ). Untuk s > 1 , siri menumpu dan ζ ( s )> 1. Penerusan analisis di sekeliling tiang pada s = 1membawa kepada rantau nilai negatif, termasuk ζ (-1) = -  1/12

Dalam regulatariasi fungsi zeta , siri ini $$ {\ displaystyle \ sum _ {n = 1} ^ {\ infty} n} digantikan oleh siri ini $$ {\ displaystyle \ sum _ {n = 1} ^ {\ infty} n ^ {- s}} . Siri terakhir adalah contoh siri Dirichlet . Apabila bahagian sebenar s lebih besar daripada 1, siri Dirichlet menumpu, dan jumlahnya ialah fungsi Riemann zeta ζ ( s ). Sebaliknya, siri Dirichlet akan menyimpang apabila bahagian sebenar s adalah kurang daripada atau sama dengan 1, jadi, khususnya, siri 1 + 2 + 3 + 4 + ⋯ yang dihasilkan dari tetapan s = -1 tidak berkumpul . Manfaat untuk memperkenalkan fungsi Riemann zeta ialah ia boleh ditakrifkan untuk nilai-nilai lain s dengan meneruskan analitik . Seseorang kemudiannya boleh menentukan zeta-regularized jumlah 1 + 2 + 3 + 4 + ⋯ untuk menjadi ζ (-1).

Dari sudut ini, terdapat beberapa cara untuk membuktikan bahawa ζ (-1) = -  1/12 . Satu kaedah, sepanjang garis penalaran Euler, ^[11] menggunakan hubungan antara fungsi Riemann zeta dan fungsi Dirichlet dan η ( s ). Fungsi itu ditakrifkan oleh siri Dirichlet yang bergantian, jadi kaedah ini sama dengan heuristik yang lebih awal. Di mana kedua-dua siri Dirichlet berkumpul, satu mempunyai identiti:

 {\ displaystyle {\ begin {alignedat} {7} \ zeta {s} +2 ^ {- s} && {} + 3 ^ {- s} + 4 ^ { s} && {} + 5 ^ {- s} +6 ^ {- s} + \ cdots & \\ 2 \ times 2 ^ {- s} \ zeta (s) & {} = {} & 2 \ times 2 ^ {- s} && {} + 2 \ times 4 ^ {- s} && {} + 2 \ times 6 ^ {- s} + \ cdots & \\\ left (1-2 ^ {1-s} kanan) \ zeta (s) & {} = {} & 1 ^ {- s} -2 ^ {- s} && { -s} -6 ^ {- s} + \ cdots & = \ eta (s) \\\ end {alignedat}}}

Identiti $$ {\ displaystyle (1-2 ^ {1-s}) \ zeta (s) = \ eta (s)} terus memegang apabila kedua-dua fungsi dilanjutkan dengan kesinambungan analisis untuk memasukkan nilai s yang mana siri di atas menyimpang. Substituting s = -1 , satu mendapat -3 ζ (-1) = η (-1).Sekarang, pengiraan η (-1) adalah satu tugas yang lebih mudah, kerana fungsi tersebut sama dengan jumlah Abel dari siri penentuannya, ^[12] yang merupakan had satu segi :

$$ {\ displaystyle -3 \ zeta (-1) = \ eta (-1) = \ lim _ {x \ to 1 ^ {-}} \ left (1-2x + 3x ^ {2} -4x ^ {3} + \ cdots \ right) = \ lim _ {x \ to 1 ^ {-}} {\ frac {1} {{\ frac {1} {4}

Membahagikan kedua belah pihak dengan -3, satu mendapat ζ (-1) = -  1/12 .

Penyusunan semula cutoff [ sunting ]

Siri 1 + 2 + 3 + 4 + ⋯

Selepas melicinkan

Tingkah laku asimtotik yang melicinkan. The y -intercept parabola adalah -  1/12 . ^[1]

Kaedah regularization menggunakan fungsi cutoff boleh "melicinkan" siri untuk tiba di -  1/12 . Pelicin adalah jambatan konseptual antara fungsi zeta regularization, dengan pergantungannya pada analisis kompleks , dan penjumlahan Ramanujan, dengan cara pintasnya untuk formula Euler-Maclaurin . Sebaliknya, kaedah ini beroperasi secara langsung pada transformasi konservatif siri ini, menggunakan kaedah dari analisis sebenar .

Idea ini adalah untuk menggantikan siri diskrit yang berperilaku buruk $$ {\ displaystyle \ sum _ {n = 0} ^ {N} n} dengan versi smoothed

$$ {\ displaystyle \ sum _ {n = 0} ^ {\ infty} nf \ left ({\ frac {n} {N}} \ right)} ,

di mana f adalah fungsi cutoff dengan sifat yang sesuai. Fungsi cutoff mesti dinormalisasikan kepada f (0) = 1 ; ini adalah normalisasi yang berbeza daripada yang digunakan dalam persamaan kebezaan. Fungsi cutoff harus mempunyai derivatif yang dibatasi cukup untuk melicinkan kedutan dalam siri ini, dan ia harus reput hingga 0 lebih cepat daripada siri yang tumbuh. Untuk kemudahan, seseorang mungkin memerlukan f adalah licin , dibatasi , dan disokong dengan ringkas .Seseorang kemudiannya boleh membuktikan bahawa jumlah pelicin ini adalah asimtotik kepada -  1/12 + CN ² , di mana C adalah pemalar yang bergantung kepada f . Tempoh berterusan pengembangan asymptotic tidak bergantung kepada f : ia semestinya nilai yang sama yang diberikan oleh kesinambungan analitik, -  1/12 . ^[1]

Penjumlahan Ramanujan [ sunting ]

Jumlah Ramanujan 1 + 2 + 3 + 4 + ⋯ juga -  1/12 . Ramanujan menulis dalam surat keduanya kepada GH Hardy , bertarikh 27 Februari 1913:

"Dear Sir, saya sangat bersyukur kerana membaca surat anda pada 8 Februari 1913. Saya menjangkakan balasan daripada anda sama dengan yang Profesor Matematik di London menulis meminta saya untuk mengkaji dengan teliti Bromwich 's Infinite Series dan tidak jatuh ke dalam perangkap siri divergent .... Saya memberitahunya bahawa jumlah nombor tak terhingga siri tak terhingga: 1 + 2 + 3 + 4 + ⋯ = -  1/12 di bawah teori saya. Sekiranya saya memberitahu anda ini, anda akan segera memberitahu saya bahawa suaka gila sebagai matlamat saya. Saya melebarkan ini hanya untuk meyakinkan anda bahawa anda tidak akan dapat mengikuti kaedah saya bukti jika saya menunjukkan garis yang saya meneruskan dalam satu huruf. ... " ^[13]

Penjumlahan Ramanujan adalah satu kaedah untuk mengasingkan istilah tetap dalam formula Euler-Maclaurin untuk jumlah separa siri. Untuk fungsi f , jumlah Ramanujan klasik siri ini $$ {\ displaystyle \ sum _ {k = 1} ^ {\ infty} f (k)} didefinisikan sebagai

$$ {\ displaystyle c = - {\ frac {1} {2}} f (0) - \ sum _ {k = 1} ^ {\ infty} {\ frac {B_ {2k}} {(2k)!} f ^ {(2k-1)} (0),}

di mana f ^(2 k -1) adalah derivatif (2 k - 1) -th daripada f dan B _2 k ialah bilangan k 2 Bernoulli : B ₂ = 1/6, B ₄ = -  1/30 , dan sebagainya. Menetapkan f ( x ) = x , derivatif pertama f ialah 1, dan setiap istilah lain akan hilang, jadi: ^[14]

$$ {\ displaystyle c = - {\ frac {1} {6}} \ times {\ frac {1} {2}} = - {\ frac {1} {12}}.}

Untuk mengelakkan ketidakkonsistenan, teori moden Ramanujan mengisyaratkan bahawa f adalah "biasa" dalam erti kata bahawa derivatif pesanan yang lebih tinggi dari keruntuhan f dengan cukup cepat untuk terma selebihnya dalam formula Euler-Maclaurin untuk cenderung 0. Ramanujan diam-diam menganggap ini harta. ^[14] Syarat keteraturan menghalang penggunaan penjumlahan Ramanujan pada siri spasi seperti 0 + 2 + 0 + 4 + ⋯ , kerana tiada fungsi tetap mengambil nilai tersebut. Sebaliknya, siri sedemikian mesti ditafsirkan oleh regulatariasi fungsi zeta. Atas sebab ini, Hardy mengesyorkan "berhati-hati" apabila menggunakan siri Ramanujan siri yang diketahui untuk mencari jumlah siri yang berkaitan. ^[15]

Kegagalan kaedah penjumlahan linear stabil

Kaedah penjumlahan yang bersifat linear dan stabil tidak boleh menyimpulkan siri 1 + 2 + 3 + ⋯ ke mana-mana nilai terhingga. (Stabil bermakna menambah istilah pada awal siri meningkatkan jumlah dengan jumlah yang sama.) Ini dapat dilihat seperti berikut. Jika

1 + 2 + 3 + ⋯ = x

kemudian menambah 0 kepada kedua belah pihak

0 + 1 + 2 + ⋯ = 0 + x = x dengan kestabilan.

Oleh linier, seseorang boleh menolak persamaan kedua dari yang pertama (tolak setiap komponen baris kedua dari baris pertama dalam lajur) untuk memberi

1 + 1 + 1 + ⋯ = x - x = 0.

Menambah 0 kepada kedua-dua pihak sekali lagi memberi

0 + 1 + 1 + 1 + ⋯ = 0,

dan menolak dua siri terakhir yang diberikan

1 + 0 + 0 + ⋯ = 0

bertentangan dengan kestabilan.

Kaedah yang digunakan di atas kepada jumlah 1 + 2 + 3 + ⋯ sama ada tidak stabil atau tidak linear.

Fizik 

Dalam teori string bosonik , percubaan ini adalah untuk mengira tahap tenaga mungkin rentetan, khususnya tahap tenaga terendah. Bercakap secara tidak rasmi, setiap harmonik rentetan itu dapat dilihat sebagai kumpulan D - 2 osilator harmonik kuantum independen, satu untuk setiap arah melintang , di mana D adalah dimensi ruang masa. Jika frekuensi ayunan asas ialah ω maka tenaga dalam pengayun yang menyumbang kepada harmonik n adalah n/2 . Oleh itu, menggunakan siri penyelarasan, jumlah keseluruhan harmonik adalah -  ( D - 2)/24 . Akhirnya ia adalah fakta ini, digabungkan dengan teorem Goddard-Thorn , yang membawa kepada teori string boson yang gagal konsisten dalam dimensi selain daripada 26. ^[16]

Pengaturalan 1 + 2 + 3 + 4 + ⋯ juga terlibat dalam mengira daya Casimir untuk medan skalar dalam satu dimensi. ^[17] Fungsi pemotongan eksponen cukup untuk melancarkan siri ini, yang mewakili hakikat bahawa mod-mod tenaga sewenang-wenangnya tidak disekat oleh plat yang mengendalikan. Simetri spatial masalah ini bertanggungjawab untuk membatalkan tempoh kuadratik pengembangan. Semua yang tersisa adalah istilah yang berterusan -  1/12 , dan tanda negatif hasil ini mencerminkan fakta bahawa daya Casimir menarik. ^[18]

Pengiraan yang sama terlibat dalam tiga dimensi, menggunakan fungsi zeta Epstein sebagai pengganti fungsi Riemann zeta.^[19]

Sejarah [ sunting ]

Tidak jelas sama ada Leonhard Euler menyimpulkan siri ini -  1/12 . Menurut Morris Kline , kerja awal Euler pada siri divergent bergantung kepada pengembangan fungsi, dari mana dia menyimpulkan 1 + 2 + 3 + 4 + ⋯ = ∞ . ^[20] Menurut Raymond Ayoub, fakta bahawa siri zeta yang berbeza tidak dapat dihalang oleh Abel Euler daripada menggunakan fungsi zeta secara bebas sebagai fungsi itu, dan dia "tidak dapat melampirkan makna" kepada siri ini. ^[21] Pengarang lain telah mengiktiraf Euler dengan jumlah itu, menunjukkan bahawa Euler akan memperluaskan hubungan antara fungsi zeta dan eta kepada integer negatif. Dalam kesusasteraan utama, siri 1 + 2 + 3 + 4 + ⋯ disebut dalam penerbitan 1760 Euler De seriebus divergentibusbersamaan dengan siri geometri yang berbeza 1 + 2 + 4 + 8 + ⋯ . Euler mengisyaratkan bahawa siri jenis ini mempunyai jumlah yang terbatas dan negatif, dan dia menerangkan apa yang dimaksudkan dengan siri geometri, tetapi dia tidak kembali untuk membincangkan 1 + 2 + 3 + 4 + ⋯ . Dalam penerbitan yang sama, Euler menulis bahawa jumlah 1 + 1 + 1 + 1 + ⋯ tidak terhingga. ^[25]

Dalam media yang popular [ sunting ]

Novel David Leavitt 2007 The Kerani India merangkumi adegan di mana Hardy dan Littlewood membincangkan makna siri ini.Mereka menyimpulkan bahawa Ramanujan telah menemukan semula ζ (-1), dan mereka mengambil "suaka gila" dalam surat keduanya sebagai tanda yang Ramanujan bersentuhan dengan mereka. ^[26]

Simon McBurney 's 2007 bermain Nombor Hilang memfokuskan pada siri dalam kejadian pembukaan. Watak utama, Ruth, berjalan ke ruang kuliah dan memperkenalkan idea tentang siri berbeza sebelum menyatakan, "Saya akan menunjukkan kepada anda sesuatu yang sangat mendebarkan," iaitu 1 + 2 + 3 + 4 + ⋯ = -  1/12 . Apabila Ruth melancarkan derivasi persamaan fungsional fungsi zeta, seorang pelakon lain menujukan penonton, mengakui bahawa mereka adalah pelakon: "Tetapi matematik adalah nyata, ia menakutkan, tetapi ia adalah nyata." ^[27] [28]

Pada bulan Januari 2014, Numberphile menghasilkan video YouTube pada siri ini, yang mengumpulkan lebih daripada 1.5 juta paparan pada bulan pertama. ^[29] Video 8 minit itu disampaikan oleh Tony Padilla, seorang ahli fizik di University of Nottingham . Padilla bermula dengan 1 - 1 + 1 - 1 + ⋯ dan 1 - 2 + 3 - 4 + ⋯ dan mengaitkannya dengan 1 + 2 + 3 + 4 + ⋯menggunakan pengurangan terma-terma yang serupa dengan hujah Ramanujan. ^[30] Numberphile juga mengeluarkan versi 21-minit video yang memaparkan ahli fizik Nottingham Ed Copeland, yang menerangkan secara terperinci bagaimana 1 - 2 + 3 - 4 + ⋯ = 1/4 sebagai jumlah Abel dan 1 + 2 + 3 + 4 + ⋯ = -  1/12 sebagai ζ (-1). ^[31] Selepas menerima aduan mengenai kekurangan ketekunan dalam video pertama, Padilla juga menulis penjelasan di laman webnya yang mengaitkan manipulasi dalam video itu menjadi identiti antara kesinambungan analisis siri Dirichlet yang berkaitan. ^[32]

Dalam liputan New York Times video Numberphile, ahli matematik Edward Frenkel berkomentar, "Pengiraan ini adalah salah satu rahsia terbaik dalam matematik. Tidak seorang pun di luar mengetahui tentangnya." ^[29]

Liputan topik ini dalam majalah Smithsonian menggambarkan video Numberphile sebagai mengelirukan, dan menyatakan bahawa tafsiran jumlah itu -  1/12 bergantung pada makna khusus untuk tanda sama , dari teknik-teknik penerusan analitik , di mana sama dengan cara dikaitkan dengan. ^[33]